Exploring Time and Space Complexities of Counting Sort

Counting sort is an algorithm that sorts an input array by counting the number of occurrences of each element in the array. It uses this count to place the elements in their correct sorted position in the output array.

It is particularly efficient when the range of the input values (k) is not significantly larger than the number of elements (n).

def counting_sort(arr):
    # Find the maximum element in the array
    max_val = max(arr)
    # Initialize a count array with zeros
    count = [0] * (max_val + 1)

    # Count occurrences of each element in the input array
    for num in arr:
        count[num] += 1

    # Build the output array using the count array
    output = []
    for i in range(len(count)):
        output.extend([i] * count[i])
    
    return output

#include <vector>
#include <algorithm>
using namespace std;

vector<int> counting_sort(const vector<int>& arr) {
    // Find the maximum element in the vector
    int max_val = *max_element(arr.begin(), arr.end());
    vector<int> count(max_val + 1, 0);
    vector<int> output;

    // Count occurrences of each element
    for (const auto& num : arr) {
        count[num]++;
    }

    // Build the output array using the count array
    for (int i = 0; i <= max_val; ++i) {
        while (count[i]--) {
            output.push_back(i);
        }
    }

    return output;
}

Time Complexity of Counting Sort

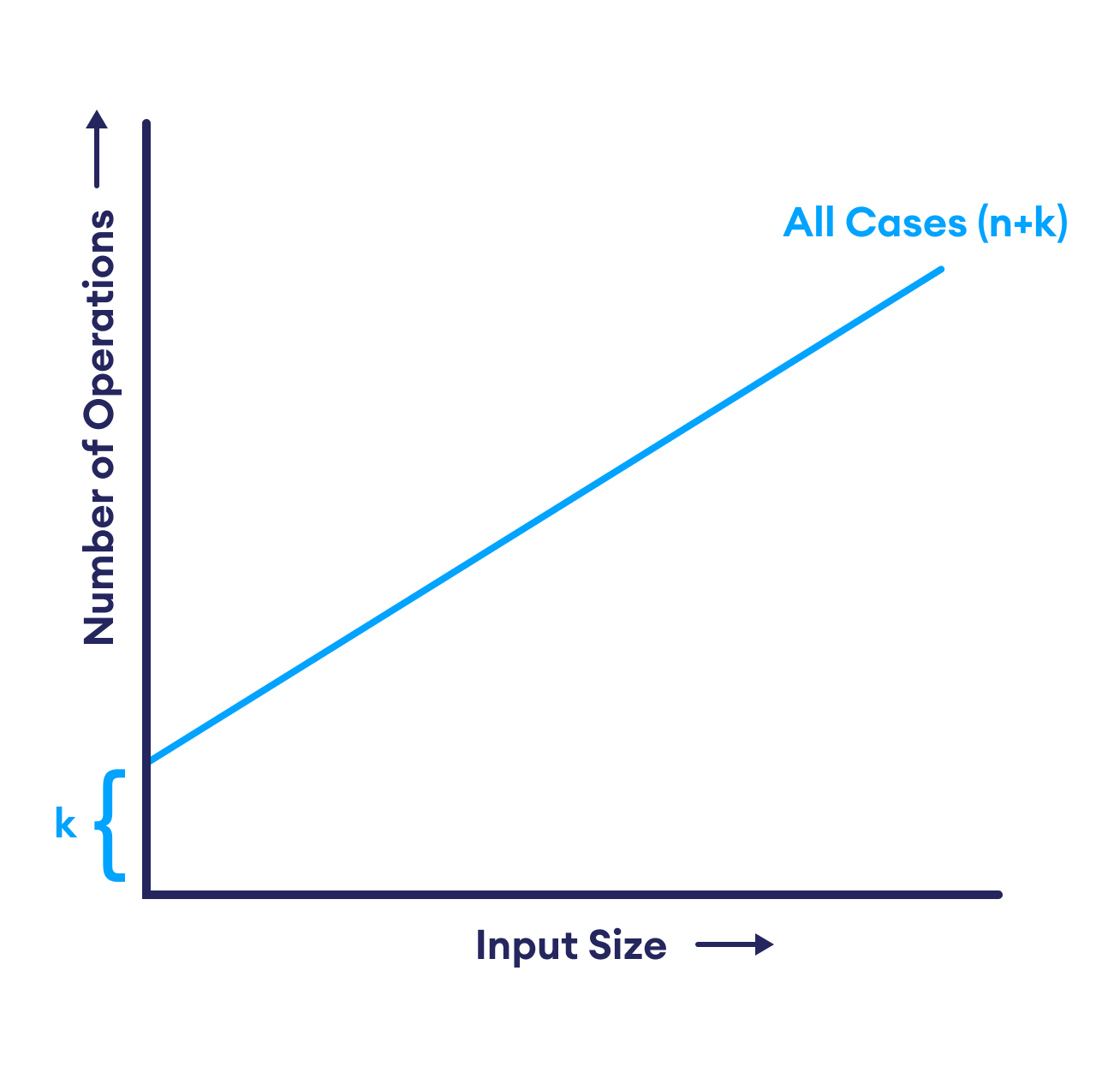
Average Case Time Complexity: O(n + k)

In all cases, the algorithm still performs the same number of operations regardless of the input's distribution. Thus, the time complexity for all cases is O(n + k), where

• n is the number of elements.
• k is the range of the input values.

Consider the following array:

2, 3, 1, 4, 2, 3, 1

1. Counting the Elements

First, the algorithm initializes an array of size k+1 and then updates it with the cumulative occurrences of each element in the range (k = 4):

Here, each operation has a time complexity of O(k).

2. Building the Output

The algorithm then constructs the output array using the count array:

1, 1, 2, 2, 3, 3, 4

This operation has a time complexity of O(n).

So, regardless of the distribution of values, the total time complexity is O(n + k).

Space Complexity of Counting Sort: O(n + k)

Counting sort requires two main arrays: the count array and the output array. In this algorithm:

• The size of the count array is determined by the range of the input values (k).
• The output array is proportional to the number of elements (n).

Thus, the space complexity is O(n + k).

Summary: Time and Space Complexity

Here,

• n - The total number of elements to be sorted.
• k - The range of the input values.

When to Use Counting Sort?

Counting sort is not a comparison-based sorting algorithm, making it very efficient when the range of input values (k) is not excessively larger than the number of elements (n).

It is particularly useful for sorting integers or categorical data.

When to Use:

1. For Input Values with Small Range: Counting sort is ideal when k is not much larger than n. For example, sorting numbers between 0 and 1000.
2. Sorting Integers or Categorical Data: Counting sort works best with discrete values (such as integers or other discrete categories).

When to Avoid:

1. Large Range of Values: If k is significantly larger than n, counting sort can consume too much memory and become inefficient.
2. Non-Integer Data: Counting sort works only for discrete data like integers. It is not suitable for floating-point numbers or other non-integer types.